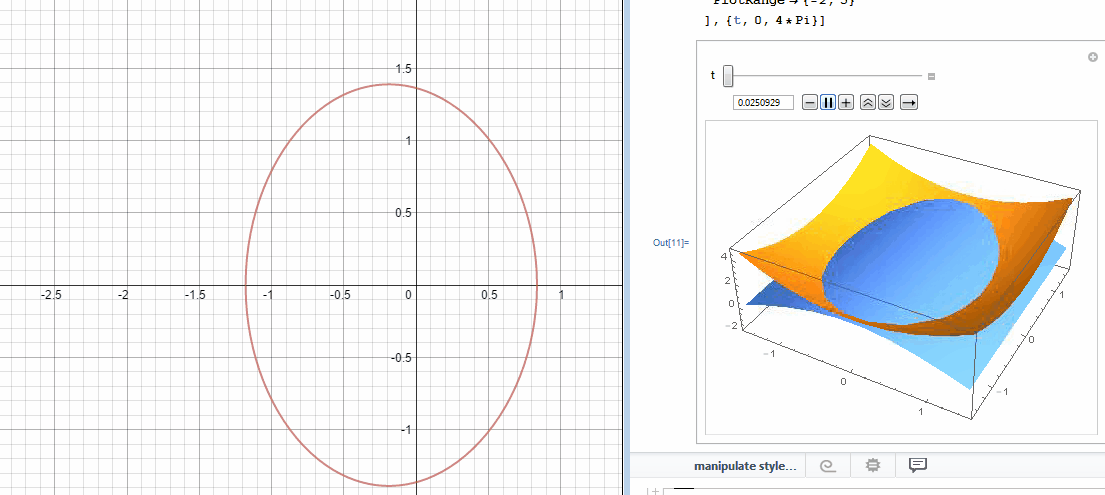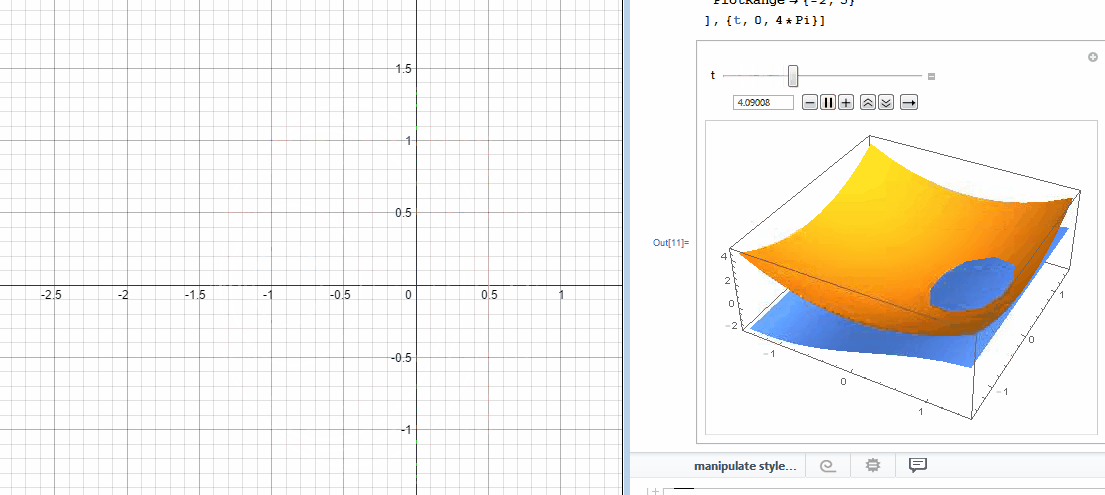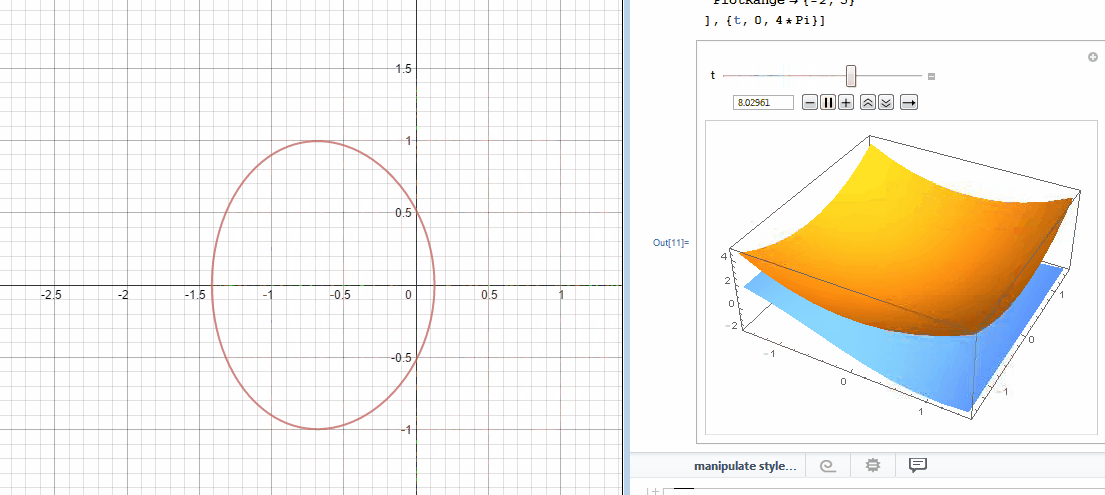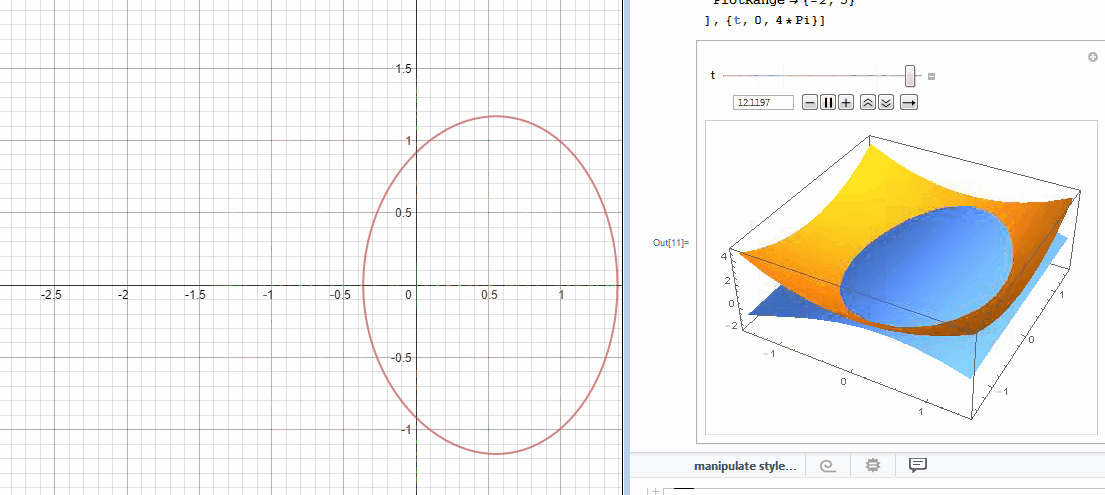
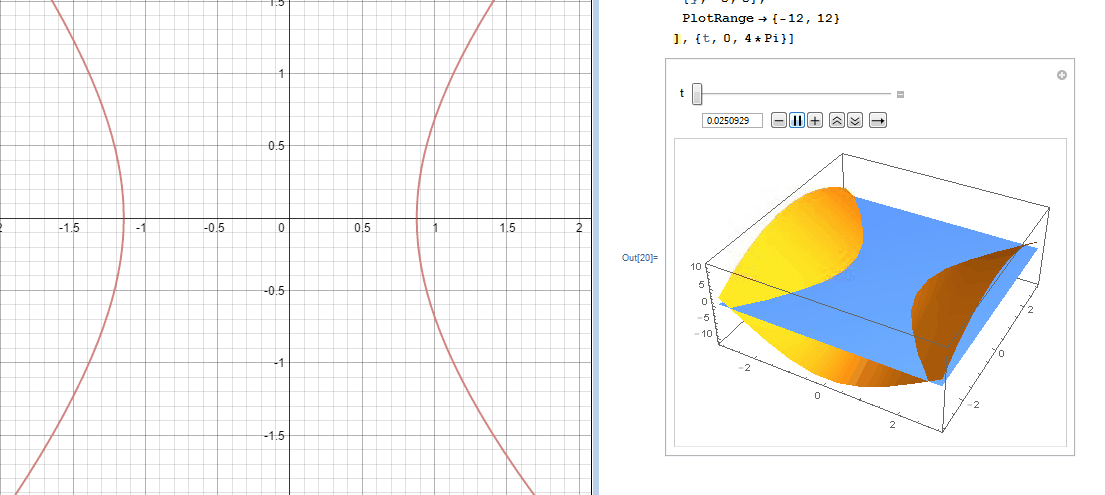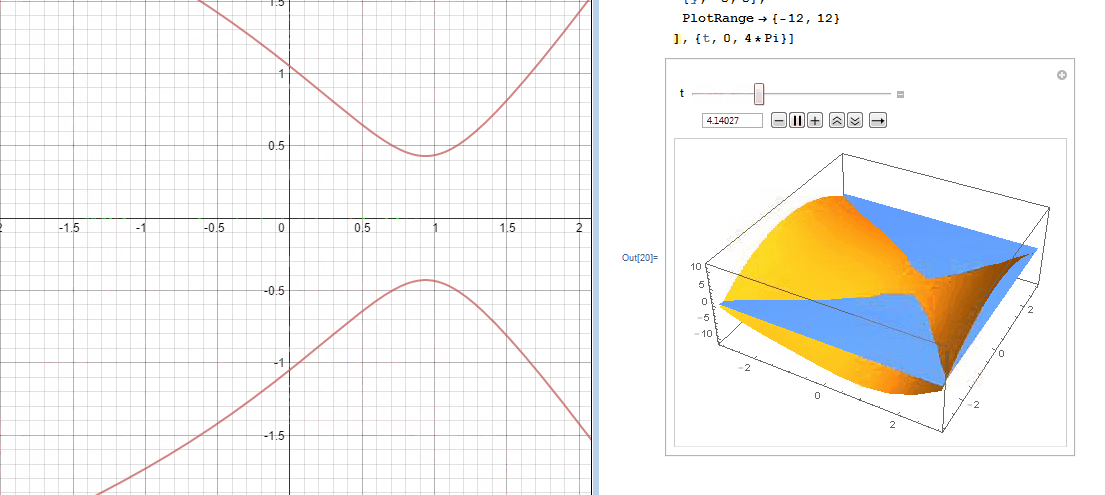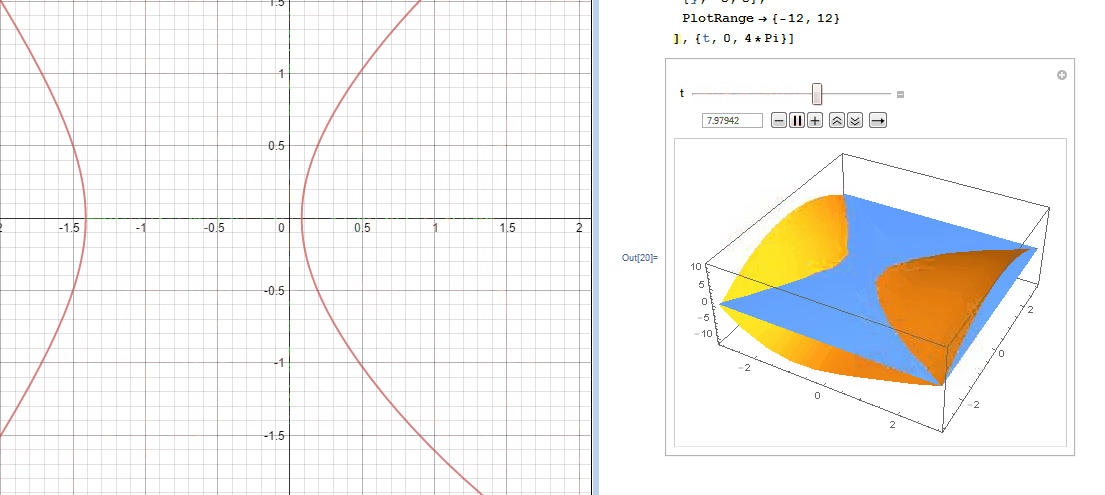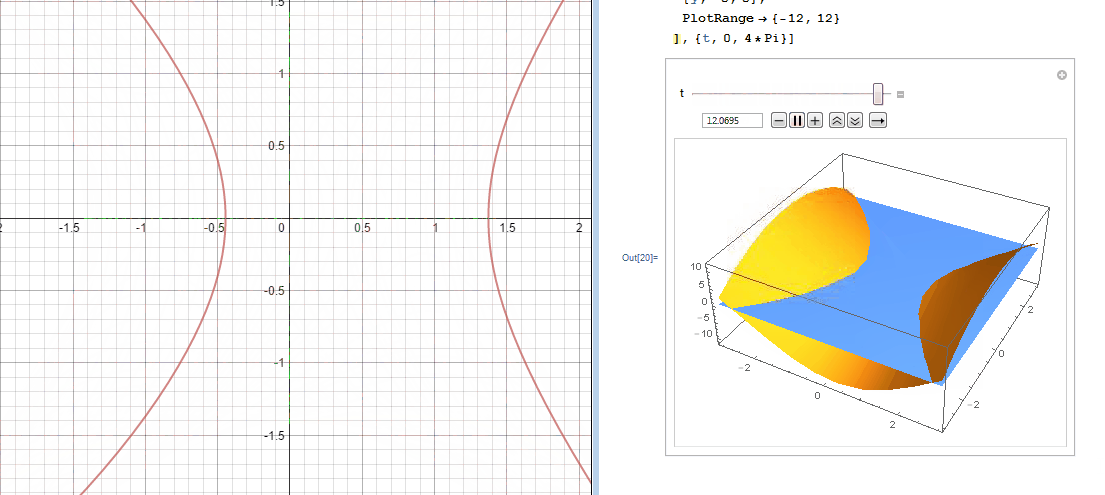
In an effort to better understand the two desmos graphs below I used Mathematica to create 3D models.
|
The site does have a demo version of Graphing Calculator that you can try out for free to see what the program has to offers. For anyone that has found desmos and geogebra to be limiting this program might what you are looking for. I have found that it renders most 3D objects quicker than Mathematica and has simplified the tools needed for manipulating 3D graphs. All of the graphs that I showed in the video are included with the demo version of the software along with many more.
The website for Graphing Calculator https://www.pacifict.com/ Ch: 7 - Knowing, Making, and Playing
Quote: "Being able to find Iraq on a map was not a what question to them, it was a where question, which could be answered quickly and in very detailed ways." I think that this quote really hits on one of the major transitions that is occurring in education and a significant hurdle new teachers face when dealing with seasoned teachers. It's always been the goal of education to have students understand how to solve problems. Before we had constant assess to the internet this meant that you had to memorize a significant amount of information. In the new information age the amount of knowledge that must be rote memorized has significantly shrunk however not all lessons and teachers have adjusted to this transition. Question: What is the base level of information that a student must have memorized for the world today? I feel that there are some equations and information that people should know just in case. Everyone should know their Social Security Number since it's impractical to keep in on you. Everyone should understand basic multiplication and unit conversion since it's important for quickly calculating distance, length and travel time. A functional understanding of money and credit should be required knowledge. With the focus on the thousands of little standards that make up each subject I have seen students who have lacked a functional understanding of these core ideas. Connection: I have repeatedly read in this program how students need to practice understanding. To often we start solving problems before we understand what they are asking. This chapter highlights this idea since it focuses on how students prioritize and evaluate problems. They have taken problems and re-contextualized them so that they are solvable within their framework. Students understand the tools they have available with the internet and they would be better served if we helped them to find better tools and understand what their tools are doing. I want students to understand how to solve problems not how to find solutions in the back of the book or on a webpage. Epiphany/Aha: Agency and play were large Aha moments for me. I have repeatedly told people that the hardest part of planning is trying to find a way to create a lesson that will generate flow with 30 students. I find that flow occurs when the difficulty of a problem is such that I know I can solve it but that it will take work. When I have no idea were to start I get distracted and discouraged, when it's too easy I put it off, when it's boring it's probably one or both of these. I have solved plenty of problems that I didn't need to specifically because they looked difficult but solvable. Trying to design a lesson that will have that level of difficulty to solvability for 30 students is an ongoing struggle. Ch: 8 - Hanging out, Messing Around, and Geeking Out Quote: "When messing around, young people begin to take an interest in and focus on the workings and content of the technology and media themselves, tinkering, exploring, and extending their understanding." I feel that this is the level education should always be striving for. We should be trying to assist students in understanding technology and tools so that they can begin to utilize them to create and explore. Question: What is the best way to assist with leading students towards geeking out about a subject? Students already geek out about subjects they are interested in. Something has previously hooked them into surfing/skating/videogames/etc and they are actively pursuing videos and information about those subjects. Finding material in that standard curriculum that can engage students is difficult. Connection: I have found in my Business Math class I have been able to occasionally engaged some students at a deeper geeking out level. Ether the material connected with a plan or idea they had, or they saw a difficult problem they felt they could solve, I have had some students spend extra time working on problems trying to understand them at a deeper level. Trying to piece together why something works instead of just taking it for granted. Epiphany/Aha: I feel that the discussion of messing around was insightful. I have previously described to people the ideal difficulty for problems that we should be giving students, however this chapter introduced the idea that it familiarity with tools and knowledge is also important. Students need to be truly comfortable with their knowledge before they can start experimenting with it in solving problems. Ch: 9 - The New Culture of Learning For A World Of Constant Change Quote: "As we have seen, tacit learning functions most effectively when students discover their own learning objectives. Games, which allow learners to play, explore, and experience, also allow them to discover what is important to them, what it is they actually want to learn - and that keeps them playing." The push for students centered self-learning has been a major one in my mathematical methods class. We have repeated touched on the importance of students creating meaning and knowledge. Lessons where students create connections stay in the students memorizes longer and can be built upon more readily. If we want students to see the connections between different problems they need to discover and construct solutions to the problems. Question: What tools are currently available that assist with gamification of learning? I remember being drawn into simple early 90's educational computer games for reading and math however I'm not sure that I have seen a major growth in that area. I know that we have collected a lot of data on how students learn and I understand that the ALEKs software package has a strong understanding of how mathematical topics relate and build on each other. However I have yet to see an engaging and fun game built on these systems. I'm sure that some company is working on a method for achieving this goal, I just haven't heard about it yet. Connection: I have played WoW on and off since it launched and have dipped my toe in most major MMO's made in the last 16 years. I can definitely see connections to the idea of building understanding and flow in these environments. I have spent time on the Elitist Jerks forum looking at data for priest specs. I have always wondered how deep this type of focus goes though. I enjoy the numbers and stats that we displayed however I know that some people only skimmed the articles and read the conclusion and followed the listed spec. There is a similar concept in Magic the Gathering where some players will dig deep into the game and examine synergies and combinations while others will just buy the cards that are listed and follow the directions. Even in groups made up of highly engaged and inquisitive individuals their are still members that are only looking for a solution or formula. Epiphany/Aha: I think the realization that there is a connection between those people who will play a game but never really look into it and students who will follow formulas but never understand them was a major epiphany for me. I've been surprised at calculus and statistics students who can get through a class without understanding the material before. The have found a way to min/max math education. They understand that normal AP calculus and statistics only requires an understanding of the formulas. A quick google search will find enough example problems that it quickly becomes an exercise in pattern recognition. They are displaying intelligence in how they find and memorize standard solutions, they just aren't displaying the intelligence that we expect or were planning for. Conclusion: Overall I really enjoyed this book. It had some insightful views on integration of technology into curriculum and reinforced some of my views about how students should be introduced to material and taught. I was able to finish 38 of the 50 problems I was aiming for with this 20% project.
I found that the time I was able to commit to this project was well worth it over the course of this semester. The chance to work some interesting and original mathematical work created a nice break from the reflections and lesson planning that took up most of my time in last year. My 10 Original Questions. 1. Does Mathematica have enough built in tools to do this task? Yes. Once I started to dig into Mathematica I found that it had a wealth of built in functions. Most of my struggle has come from selecting the correct tool to use when their is more than one available. 2. Does my knowledge of C++ transfer to Mathematica? Not as much as I had hoped it would. The built in functions actually move me away from the structure and design of C++. I found that designing an algorithm in Mathematica is much more time consumming than in C++. Usually I ended up finding a function that would effectively do what my own algorithm design would have done, just much faster. 3. How long will it take to get competent with Mathematica? I'm still not competent with Mathematica. I can graph functions and generate series and lists quickly now, however I still struggle with the deeper material. I still have to look up most functions to remember all of their components. 4. How difficult is it to create functional algorithms in Mathematica? Around medium difficultly. The process isn't that bad, but you need to have a strong foundational understanding of exactly what you want the algorithm to do. I found that I had much more success piecing together algorithms in C++ than Mathematica because of the structure of the language. 5. Are there coding considerations I should be aware of when working with Mathematica? Not as many as C++. They both have similar coding requirements for their built in functions so you can't be that loose with the code structure. However the list focus of Mathematica is different than C++ so some of the array operations have been drastically simplified. 6. How difficult of a task have I set for myself? I think that the problem was actually really appropriate for me. If I had focused on this problem a little more during the semester I could have probably finished the first 100. Instead I only finished 38 problems by the end. 7. Are there classes of problems that are more difficult with Mathematica? Yes. Going through the problems I found that most of the problems that start with a long list of numbers were more difficult. The problems were generally simple once I got them into the computer with the right format, however getting them to that point was harder than I expected. Usually it took a lot of work to get it input into the system correctly. 8. Can these problems be adjusted for use in the classroom? Yes. Some of the problems have a nice structure to them and are easily understood. They fall into a category of problems that generally have a low entry requirement. Many of the problems have a repeating structure that can be easily grasped at first, finding the final solution usually takes brute force or mathematical trickery. 9. What mathematical fields are covered by this project? I have found that most of the problems in the first 50 are strictly combinatoric in nature. I have seen later problems that deal with calculus however in the first 50 it's mostly about counting. 10. How much does Mathematica cost if I decide to keep using it after this project? $235 or $135 per year.
Chimamanda does an excellent job in this TED video of describing the problems with only getting a single side of a story. When we fail to fully examine a situation we eventually end up with only a single version of the story. If we want to make informed decisions about the many topics and ideas that we are asked about daily we need to strive for a fuller understanding. Instead of giving students blanket statements that are based off of evidence we heard during a sound bit, we should dig deeper and have our students dig into questions and stories that they want to know more about. With the wealth of information available now it is a shame that we continue to take a single source as truth when we could explore and learn more with only a couple clicks of the mouse.
All of these pictures come from my old Flickr account.
I was asked by my students what I did in the Coast Guard so I showed them some photos I had taken from the air and shared this story about the flipped over NOAA buoy.
NOAA buoys are specifically designed to not flip over. Most buoys are attached to their anchor by a couple thousand pounds of chain. However NOAA buoys are usually placed in deeper water and have to use nylon rope to attach to their anchor.
Since they don't have the extra weight of the chain to assist with keeping them upright they are designed like weeble-wobbles. In the entire year I was in Alaska I only saw this one buoy flipped over so it was a semi-unique experience.
Problem 47 prob47 = Flatten[Table[Length[FactorInteger[n]], {n, 1, 200000}]]; prob47b = Table[Sum[prob47[[a + i]], {i, 0, 3}], {a, 1, 199997}]; Position[prob47b, 16] =========================== Problem 44 prob44a = Table[m*(m + 1)/2, {m, 1, 100000}]; prob44b = Table[n*(3*n - 1)/2, {n, 1, 100000}]; prob44c = Table[o*(2*o - 1), {o, 1, 100000}]; Intersection[prob44a, prob44b, prob44c] ============================ Problem 40 prob40 = Flatten[IntegerDigits[Table[n, {n, 1, 200000}]]];
Product[prob40[[10^a]], {a, 0, 6}] Ch:4 - Learning In The Collective
Quote: "This core aspect of education in the new culture of learning presents a model for understanding learning in the face of rapid change. Teachers no longer need to scramble to provide the latest up-to-date information to students because the students themselves are taking an active role in helping to create and mold it, particularly in areas of social information." Question: This chapter focuses on the idea of collectives as an avenue for learning and gives examples of how groups can come together to expand their knowledge. My question is can collectives be leveraged to bring about structured learning? How would you structure a question or problem such that a collective would be the best method for solving it? Connection: I have made heavy use of the collectives available on stackexchange throughout my 20% project and my degree. This site has specific subgroups of professionals that have provided years worth of answers to questions and have been able to direct me to solutions when I have asked for assistance. I understand the power of collaborative groups like this, however I am highly inquisitive and self study regularly. I'm not sure how I could translate the use and worth of these types of sites to students who are truly disengaged with math. Epiphany/Aha: The last paragraph of the chapter actually answers my initial question. These collectives are powerful tools that students should know about and be familiar with, however trying to focus them and direct them towards traditional models of education will be ineffective. These types of learning environments will always be too fluid to allow for traditional learning objectives and goals. Ch:5 - The Personal With The Collective Quote: "The learning that happens through blogs, social networks, and other new media may be deeply grounded in experience and personal expression, but it also arises from the contributions of multiple people and voices. Expertise and authority are dispersed rather than centralized, and once a digital space hits a point of critical mass, it is very likely that some member of the community will have valuable expertise to share about a given topic." Question: This chapter deals with blogs as a collective for pooling knowledge and skill to find solutions to problems. My question is how should you go about cultivating this pool of knowledge? While the search for interesting authors can be enlightening, it can also lead to dead ends and bad information. Without a central location to refer to it becomes difficult to find the great blogs hidden away and most people will end up concentrated around the major talking heads of any community. Connection: I have personally found some great posts about math education while searching for help with writing a lesson plan. The problem is that many of these posts are on blogs that haven't been updated in years. I feel that some of these teachers might have started out with grand ideas and some really interesting lessons and then found that the community for their ideas was too spread out and quit blogging before it had a chance to connect with anyone. Epiphany/Aha: I feel that the important take away from this chapter is the idea that we can introduce students to learning that they perceive of as fun. I have seen students work on problems that weren't assigned to them because the problems had the right ratio of difficulty to skill. I feel that students will work harder to solve a problem if they feel it is difficult but solvable than they will for a problem that is easy to solve. Striving for something that is just out of reach is much more rewarding. Creating learning environments with the tools of the new information age requires that we think of ways to implement lessons that have these qualities. Ch:6 - We Know More Than We Can Say Quote: "Yet finding answers and memorizing facts do little to inspire students' passion to learn. If anything, they dull that desire and make learning a tiresome burden." Question: How do we best go about finding and designing lessons that focus on inquiry based learning? We need questions that the students respond to and want to answer, not simply the questions we as teachers consider important. How do you direct students towards learning objectives in this systems? Connection: We focused on the idea of inquiry based learning in our mathematical methods class. The idea that students can learn and retain knowledge when they discover it through a more organic process than simply answering stock questions was a key tenet of the class. Epiphany/Aha: This chapter also touches on the idea of learning as play. I feel that this will probably be the major direction and advancement in education in the coming years as I feel that it will provide the best results for students learning and engagement. The traditional model is too boring for most students today let alone students of the past. To hold to that model will never bring the engagement that students require now. |
Mr. BrooksI am currently a Teacher Candidate at San Dieguito Academy. I completed my BS in Mathematics at CSUSM in May of 2014. Archives
May 2015
Categories |







 RSS Feed
RSS Feed
