I was helping a student in AVID with calculus homework when I confronted with the following problem.
I worked on it for probably 3 minutes before I called it and asked WolframAlpha for help. The response
Once I saw the arctan I remembered that this was a trig identity listed in the back of the book and that you needed to be memorize it. In the 2 years since Calc 3 I haven't used it so I forgot this one.
Since I have more mathematical knowledge at my disposile now than I did in during Calc 3 I thought I would dig around for a bit and try to remember why this specific identity related to the unit circle.
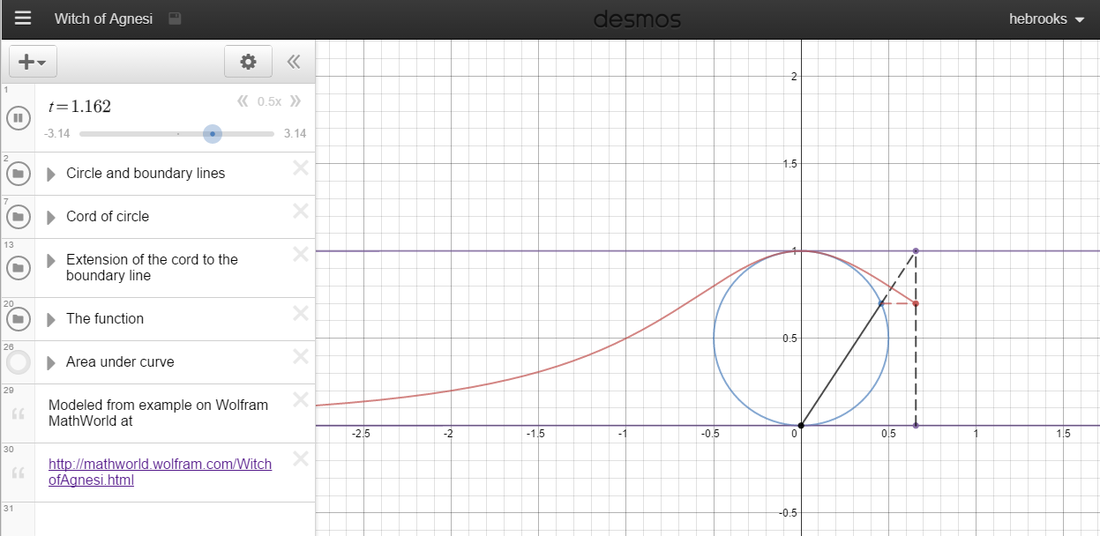
What I found was the Witch of Angensi. Having seen the curve and animation on the wiki page I then decided to try and recreate this model with Desmos.
In the end I was able to create a decent model of the Witch of Angensi and I thought I would share the process.
Since I have more mathematical knowledge at my disposile now than I did in during Calc 3 I thought I would dig around for a bit and try to remember why this specific identity related to the unit circle.
What I found was the Witch of Angensi. Having seen the curve and animation on the wiki page I then decided to try and recreate this model with Desmos.
In the end I was able to create a decent model of the Witch of Angensi and I thought I would share the process.
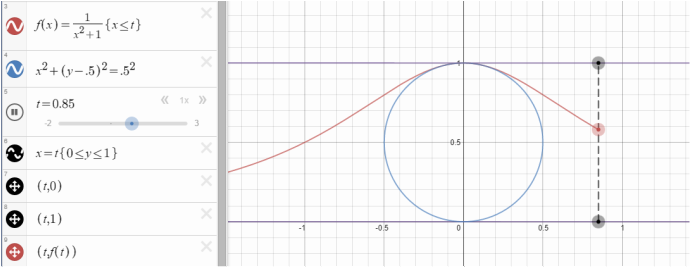
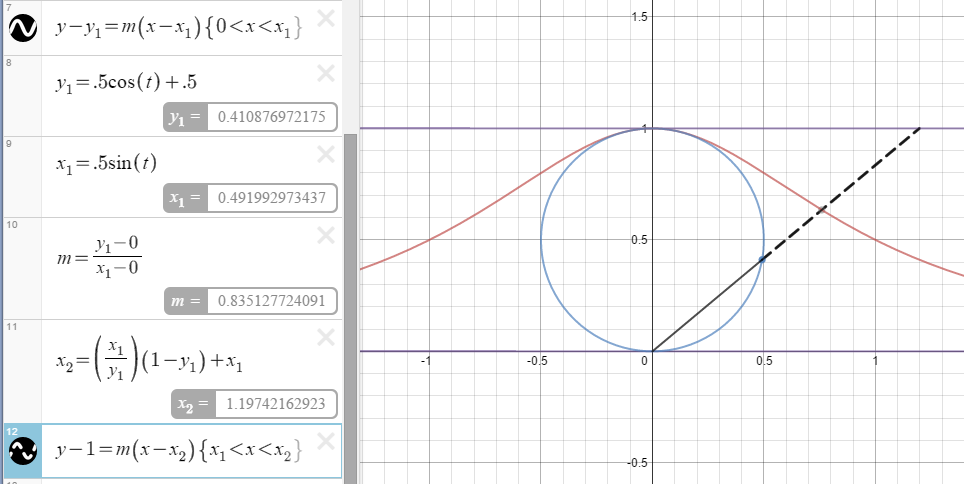
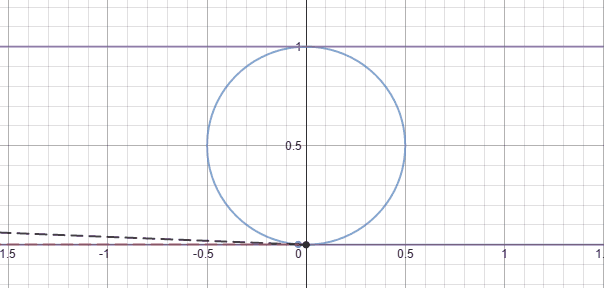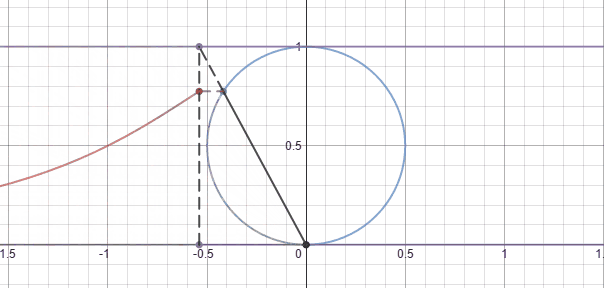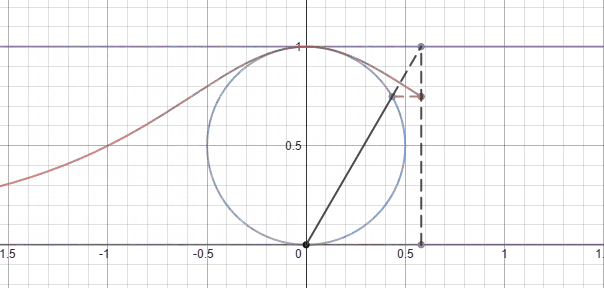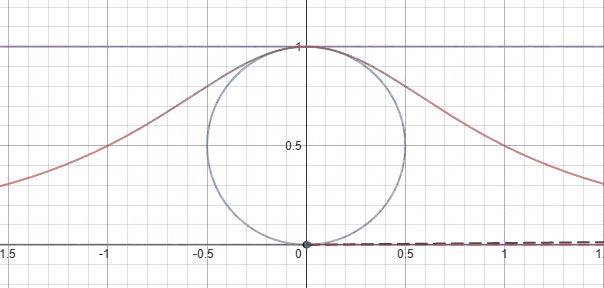
To start with I created the fixed lines and curves.
Next I created a variable t that would trace the function as it went from negative infinity to positive infinity. I also created a dashed vertical bar that would go along with the move.
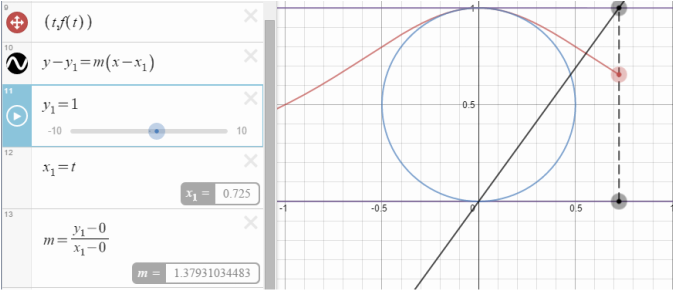
Next I had to create a line from the origin to the boundary of y=1. I used the point-slope formula for this equation.
To have the line only extend from the origin to the point (t,1) I have to add bounds to the equation using { } brackets.
Next I had to write an equation for the point of intersection between the circle and the line.
This was actually harder than I thought it would be so I decided to start with a point on the circle and then fill in the rest.
So Starting over again.
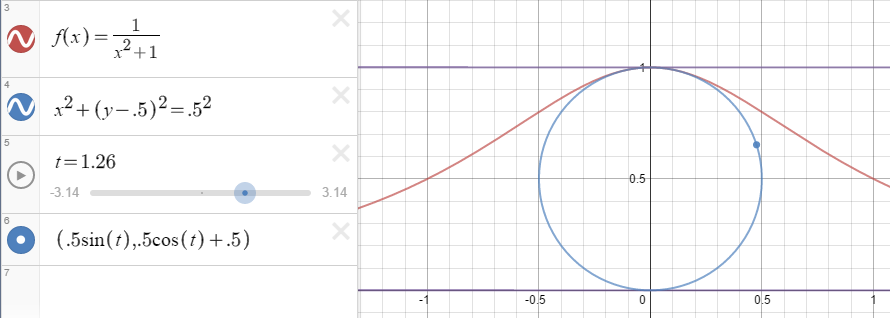
We begin by creating an equation for the point on the circle as it moves from -pi to pi.
This was actually harder than I thought it would be so I decided to start with a point on the circle and then fill in the rest.
So Starting over again.
We begin by creating an equation for the point on the circle as it moves from -pi to pi.
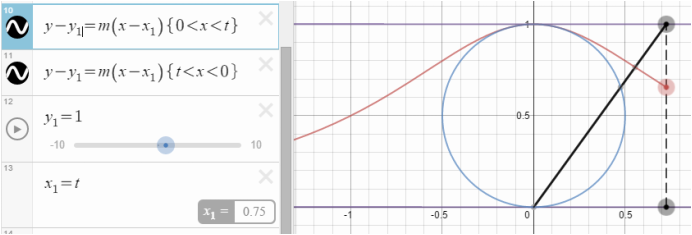
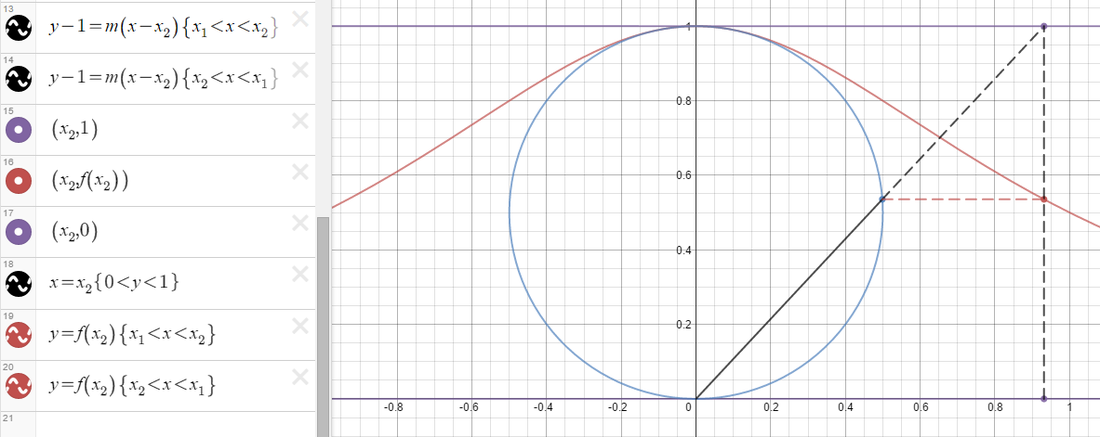
Next we again use the point slope formula to create an equation from the origin to the point on the circle and we create second equation for the line that extends from the circle to the boundary at y=1.
Using the x_2 we found in the last step we can create the other lines for the triangle.
You can now hit play on t and have a nicely animated version of the Witch of Agnesi.
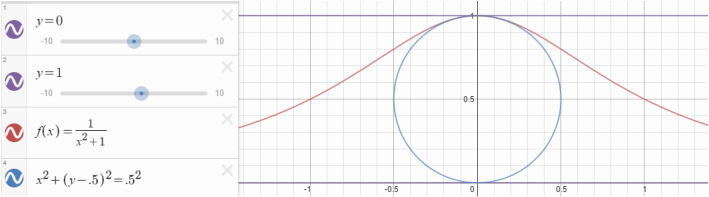
If you want to expand your knowledge you can extend this model to include different values for the radius like I did in my example at the beginning of this post.
If you want to expand your knowledge you can extend this model to include different values for the radius like I did in my example at the beginning of this post.
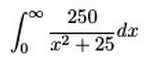
 RSS Feed
RSS Feed
