From Project Eular
Like the last problem I find it's informative to start out with an inelegant solution and try to find an elegant one at the end.
We start by generating an array of the form a^b from a=2 to 100 and b=2 to 100.
We start by generating an array of the form a^b from a=2 to 100 and b=2 to 100.
As expected that got gigantic quickly, however we don't need to look at all of the data to work with it.
We can use Flatten to compress the 99 by 99 array into a single vector 9801 elements long.
We then use DeleteDuplicates to remove all of the duplicated elements from the vector.
And finish with Length to find the total number of elements left over.
We can use Flatten to compress the 99 by 99 array into a single vector 9801 elements long.
We then use DeleteDuplicates to remove all of the duplicated elements from the vector.
And finish with Length to find the total number of elements left over.
And technically we are done. The answer to this ProjectEular problem is 9183.
However I think that it's worth while to consider why their are only 618 repeated numbers in this list.
First lets try to account for all of the numbers that are unique.
There are 25 prime numbers less than 100 and each of these numbers will generate 99 non-duplicated numbers since they will have only one number as their factor. So we have to have at least 2475 unique numbers just from the primes under 100.
However thinking about it we can also remove the numbers that are composed of primes like 6 and 15. Observe that since 6=2*3 that 6^2=(2*3)^2=2^2*3^3, and so on.
We could try to find the possible permutations of the 25 primes however there are 2^25 ways that we can combine the 25 primes and calculating which combinations have values less than 100 is rather time consuming.
Instead lets consider what numbers we know are going to show up more than once in the table?
Any number that is a power of a lower number of the list will definitely be a repeated.
The higher powers of 2 will show up in the powers of 4, 8, 16, 32, and 64.
Below I have generated a truncated list for the 2,4, and 8 table. We can see that the 4 table repeats every second value on the 2 table and that the 8 table repeats the 3rd value. This corresponds to 4=2^2 and 8=2^3.
However I think that it's worth while to consider why their are only 618 repeated numbers in this list.
First lets try to account for all of the numbers that are unique.
There are 25 prime numbers less than 100 and each of these numbers will generate 99 non-duplicated numbers since they will have only one number as their factor. So we have to have at least 2475 unique numbers just from the primes under 100.
However thinking about it we can also remove the numbers that are composed of primes like 6 and 15. Observe that since 6=2*3 that 6^2=(2*3)^2=2^2*3^3, and so on.
We could try to find the possible permutations of the 25 primes however there are 2^25 ways that we can combine the 25 primes and calculating which combinations have values less than 100 is rather time consuming.
Instead lets consider what numbers we know are going to show up more than once in the table?
Any number that is a power of a lower number of the list will definitely be a repeated.
The higher powers of 2 will show up in the powers of 4, 8, 16, 32, and 64.
Below I have generated a truncated list for the 2,4, and 8 table. We can see that the 4 table repeats every second value on the 2 table and that the 8 table repeats the 3rd value. This corresponds to 4=2^2 and 8=2^3.
I created the following two tables in Latex to highlight how the powers of 2 repeat at specific intervals in the 4 and 8 power tables. A similar pattern will occur for the powers of 3, 5, and 7.
Similarly the power table for 6 will be repeated in the power table for 36 and 10 in the power table for 100.
The following Matrix and ArrayPlot were generated in Mathematica to show the repeated numbers in the table given above. Observe that 2^6 occurs the most often in this table and is represented in black in the ArrayPlot to signify that it is a larger value.
The following Matrix and ArrayPlot were generated in Mathematica to show the repeated numbers in the table given above. Observe that 2^6 occurs the most often in this table and is represented in black in the ArrayPlot to signify that it is a larger value.
Expanding the array to include all of the numbers we originally calculated we get the following ArrayPlot. Here we see that most of the values that will have repeats are clustered around the top of the array corresponding to a values between 2 and 10.
The dark band that shows up around the 2/3 mark on the array corresponds to the powers of 2^6. As you can see by the following table the values in the 2^6 power table show up in repeatedly throughout the array.
For reference the number that shows up the most often in the table is 1152921504606846976 or 2^60. Which makes sense when you remember that 60 has 12 divisors and would thus it will show up in the power table of 2^1, 2^2, 2^3, 2^4, 2^5, 2^6.
Also you should notice that in a number of rows the values are high for half of the row and then drop down to 1 for the rest of the array. As an example the power table for 100 is at the bottom of the array window. Note that the first 50 values of this table occur in the 10 power table.
Also you should notice that in a number of rows the values are high for half of the row and then drop down to 1 for the rest of the array. As an example the power table for 100 is at the bottom of the array window. Note that the first 50 values of this table occur in the 10 power table.
It's not until 100^51 that we get the first value that doesn't show up in 10 power table.
Conclusion
This problem is mechanically simple to calculate with a computer but is calculable by hand given time and planning. I wouldn't ask students to do the full table by hand but I feel that you could probably have an interesting discussion with students concerning this material.
Conclusion
This problem is mechanically simple to calculate with a computer but is calculable by hand given time and planning. I wouldn't ask students to do the full table by hand but I feel that you could probably have an interesting discussion with students concerning this material.








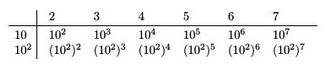
 RSS Feed
RSS Feed
